잡동사니 블로그
[LG Aimers] Module 2. Mathematics for ML - Matrix Decomposition 본문
LG AI
LG와 청년들이 함께 만드는 더 가치 있는 미래
www.lgaimers.ai
에서 진행하는 교육을 바탕으로 정리했습니다.
Determinant(행렬식) & Eigenvalue(고윳값)에 대해서
Cholesky Decomposition(숄레스키 분해)
Diagonalization (대각화),
Singular value decomposition (특잇값 분해)
1. Matrix Decomposition

#2*2 행렬 기준
import numpy as np
def inverse_Matrix(A11,A12,A21,A22):
A = np.array([[A11, A21],
[A12, A22]])
if A[0][0]*A[1][1]-A[0][1]*A[1][0] != 0 :
det_A = 1/(A[0][0]*A[1][1]-A[0][1]*A[1][0])
A_inverse=det_A*np.array([[A[1][1], -A[0][1]],
[-A[1][0], A[0][0]]])
print("---행렬---")
print(A)
print("---역행렬---")
print(A_inverse)
print("---행렬*역행렬---")
print(A_inverse@A)
inverse_Matrix(1,2,3,4)
#---행렬---
#[[1 3]
# [2 4]]
#---역행렬---
#[[-2. 1.5]
# [ 1. -0.5]]
#---행렬*역행렬---
#[[1. 0.]
# [0. 1.]]근데 Numpy에선 역행렬 구하는 코드는 한줄이면 가능
import numpy as np
A = np.array([[1, 2],
[3, 4]])
A_inverse = np.linalg.inv(A)

3*3의 matrix의 Determinant는 2*2 Determinant의 recursive formula(재귀함수)로 정의가 된다.
이것을 Laplace expansion(라플라스 전개)라고 함.
여기서 Triangular matrix(삼각행렬)는 정사각행렬의 특수한 경우로, 주대각선을 기준으로 대각항의 위쪽이나 아래쪽 항들의 값이 모두 0인 경우를 의미.
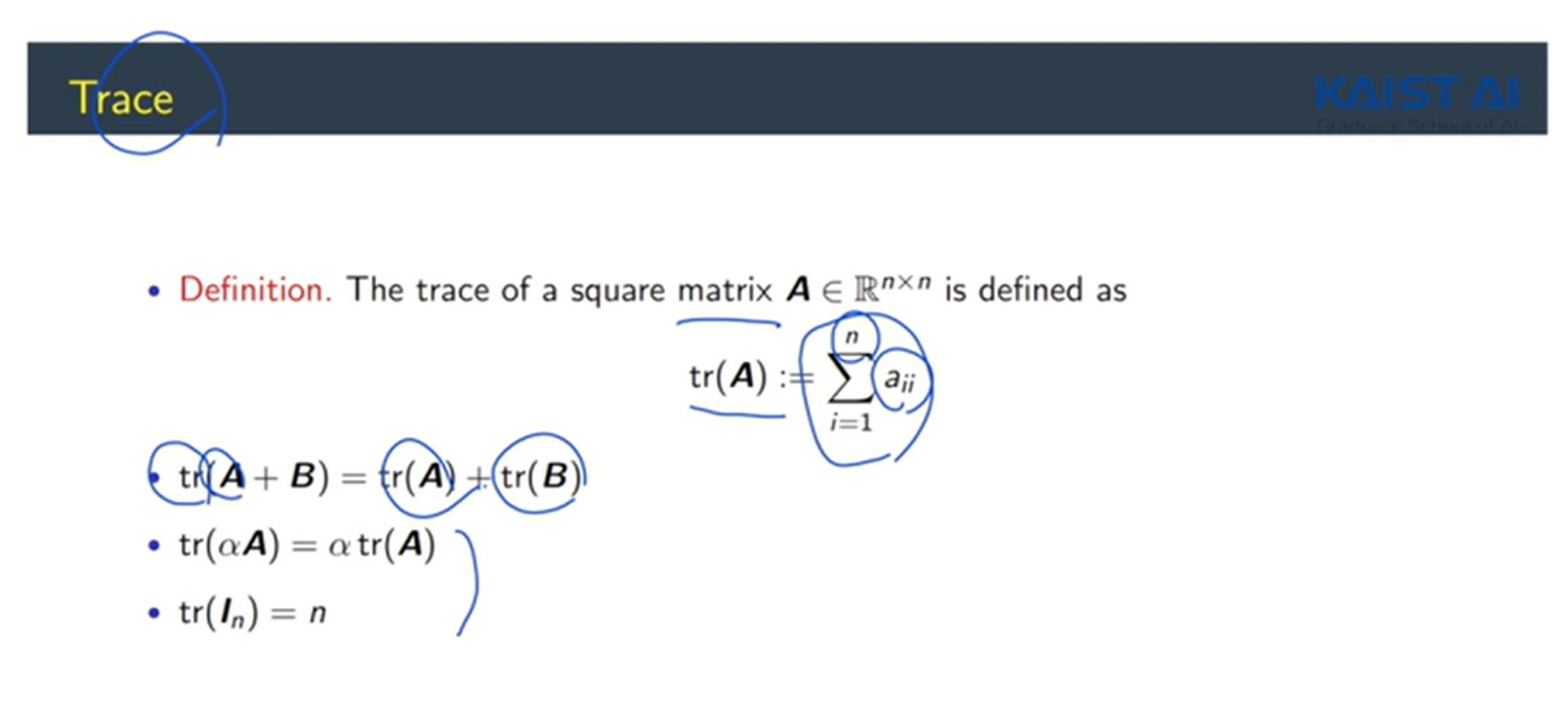
Trace(대각합)은 Determinant와 유사한 성질이 존재.

$Ax = \lambda x$
$det(A- \lambda *I_n) = 0$ 방정식 만족하면 $\lambda$가 Eigenvalue가 될 수 있음.
import numpy as np
A = np.array([[4, 2],
[1, 3]])
eigenvalues, eigenvectors = np.linalg.eig(A)
print(eigenvalues)
print(eigenvectors)
#[5. 2.]
#[[ 0.89442719 -0.70710678]
# [ 0.4472136 0.70710678]]Eigenvectors의 값이 다른 이유는 span 때문, 즉 [[2],[1]] * c 어떠한 수를 곱해도 그 Vector는 Eigenvectors가 됨.
그래서 Eigenvectors는 unique하지 않다.
Determinant는 Eigenvalue의 곱, Trace는 Eigenvalue의 합으로 표현 가능.
행렬 A가 대칭이고 모든 Eigenvalue가 0보다 크면 그 행렬은 lower-traingular matrix(하삼각행렬)와 그의 전치행렬의 곱으로 나타낼 수 있음.
이러한 이유는? Determinant 계산이 쉬워짐.

Diagonal matrix(대각행렬): Diagonal Entry만 살아있고 나머지가 전부 0인 형태.
여기서 P는 Invertible matrix(가역행렬)
Matrix A가 Symmetric(대칭)인 경우에는 어떤 A라는 Matrix는 $A = PDP^T$ 를 표현하는 P와 D가 항상 존재
Matrix가 A가 Diagonalizable하면 $1$ 와 같이 표현될 수 있고, Determinant는 $ 즉, Diagonal Matrix의 곱이 됨.
Singular value decomposition
A가 Square Matrix(정방행렬)도 아니고, Symmetric 하지도 않는 경우에 사용한다.
즉 일반적인 Matrix에 다 적용가능한 decomposition
$A = U \Sigma V^T$ 형태로 표현하는게 Singular value decomposition
$U$와 $V$는 Orthogonal matrix(직교 행렬)
$VV^T = I$
$UU^T = I$
$\Sigma$는 Diagonal Matrix
$\Sigma$의 어떤 Diagonal entry를 Singular Value라고 부름.
$U$ 는 Left Singular Vector
$V$ 는 Left Singular Vector
SVD는 항상 존재 EVD는 Symmetric Matrix(대칭행렬)이나 Square Matrix(정방행렬)에만 존재
보통은 SVD가 많이 쓰이지만 A가 Symmetric 하다면 EVD=SVD
'공부용' 카테고리의 다른 글
| Kmedoids clustering (3) | 2024.10.16 |
|---|---|
| Dice Coefficient(Dice Score) -> Dice Loss Function (1) | 2024.10.09 |
| [논문 읽기] TabTransformer: Tabular Data Modeling Using Contextual Embeddings (0) | 2023.11.16 |
| [논문읽기] TabNet: Attentive Interpretable Tabular Learning (0) | 2023.11.13 |
| [논문 읽기] Why Should I Trust You?": Explaining the Predictions of Any Classifier (0) | 2023.09.12 |




