잡동사니 블로그
[논문읽기] TabNet: Attentive Interpretable Tabular Learning 본문
https://arxiv.org/abs/1908.07442
TabNet: Attentive Interpretable Tabular Learning
We propose a novel high-performance and interpretable canonical deep tabular data learning architecture, TabNet. TabNet uses sequential attention to choose which features to reason from at each decision step, enabling interpretability and more efficient le
arxiv.org
Abstract
- Tabular data(정형데이터)에 적용이 가능하고 성능이 우수하며 동시에 해석이 가능한 표준적인 딥러닝 아키텍쳐인 TabNet을 소개함.
- Tabnet은 Sequential attention을 사용하여 각 의사 결정 단계에서 추론할 feature를 선택하고 중요한 feature에 집중하게 되어 효율적인 학습이 가능하고 interpretability(해석가능)해짐.
- 광범위한 Tabular detaset 형식에서 성능이 뛰어 났고, SSL(self-supervised learning)으로 레이블이 없는 데이터가 풍부할 때 효과를 상승 시킬 수 있음.
Introduction
- DNN(Deep Neural Network)는 이미지 텍스트 오디오 분야에서는 주목할만한 성공을 거두었음.
- 즉, raw data(원본 데이터)를 의미 있는 표현으로 인코딩 하는 아키텍쳐는 빠르게 발전.
- 그러나, Tabular data에선 아직 이러한 성공을 거두지 못했음.
- Kaggle과 같은 곳에서 앙상블 의사 결정 트리의 변형 모델들이 지배적임.
의사 결정 트리 관련 모델들이 지배적인 이유?
- Tabular data에선 흔히 볼 수 있는 hyperplane(초평면 경계)를 가지고 있는 manifolds(데이터의 공간?)에 대해 분류가 효과적.

대충 Manifold와 hyperplane은 이런 느낌[1] - 해석 가능성이 높음.
- Tree 기반 모델들은 훈련이 빠름.
MLP와 CNN같은 경우에는 지나치게 overparametrized되어 있음.
(지나치게 과도하게 파라미터화된?) 아마 딥러닝 계열 모델이 파라미터 수가 많아서 그런듯?
Tabular data에서 DNN을 사용할려는 이유?
- 대규모 데이터 셋에서 예상되는 성능 향상.
- Tree 계열 모델들과 다르게 Gradient descent (경사하강법) 기반 end-to-end 학습 지원.
- end-to-end : 입력 데이터로부터 원하는 출력 직접 얻기 위해 한 번에 모든 처리 단계를 통합하는 모델.
- tabular data 이외에도 이미지와 같은 다른 데이터와 함께 인코딩이 가능.
- feature engineering 필요성 완화.
이 논문에서는 Tabular data를 위한 새로운 표준 DNN 아키텍쳐인 TabNet을 제안하며 다음과 같이 요약됨.
- 전처리 없이 raw한 tabular data를 입력하여 Gradient descent 기반을 사용함으로 end-to-end에 유연하게 작용함.
- TabNet은 sequential attention을 사용하여 각 결정 단계에서 어떤 feature를 추론할지 선택하고 학습 때 가장 두드러진 feature가 사용됨으로 해석 가능성을 제공함과 동시에 더 나은 학습이 가능함.

- Feature의 importance와 결합 방식을 시각화 하여 지역적(local)으로 해석 가능성과 학습된 모델에 대하여 각 feature의 기여도를 정량화 하는 전역적(global) 해석 가능성을 가능하게함.
- Tabular data에 대해 처음으로 unsupervised pre-training(비지도 학습)을 사용하여 마스킹된 feature를 예측함으로써 성능 향상을 나타냄.

Related Work
Feature selection : 광범위하게 예측에 대한 유용성을 기반으로 일부 Feature를 고름.
- global methods
- forward selection (전진선택법)
- Lasso regularization (라쏘 정규화)
다르게 TabNet은 controllable sparsity(제어가능한 희소성?)을 갖춘 soft feature selection을 사용.
TabNet for Tabular Learning
- DTs(Decision Tree 계열 모델인듯)는 real world tabular data에서 성공적이였음.
- 한편으로는 DNN을 잘 설계한다면 Decision Tree와 출력이 비슷한 Manifold를 구현할 수 있음.

multiplicative sparse mask : 희소 행렬을 통해 입력 데이터 중에서 중요한 특징들만을 선택하는 역할을 하는 도구이며 이는 모델이 불필요한 정보를 무시하고, 핵심적인 정보에만 집중할 수 있게함.
-
- 처음 입력
- multiplicative sparse maskM1([x1x2])=[10][x1x2]=x1M2([x1x2])=[01][x1x2]=x2
- 가중치w와 bias추가f([x1x2])=softmax(ReLU(M1([x1x2])W1+b1)+ReLU(M2([x1x2])W2+b2))=softmax([ReLU(C1(x1−a)ReLU(−C1(x1−a)00]+([00ReLU(C2(x2−d)ReLU(−C2(x2−d)])=softmax([ReLU(C1(x1−a)ReLU(−C1(x1−a)ReLU(C2(x2−d)ReLU(−C2(x2−d)])
만약, C1≈C2이고 ∣x1−a∣≈∣x2−d∣≠0 이면 위의 함수 f의 함숫값은
f([x1x2])={[120120]T(x1>a,x2>d)[120012]T(x1>a,x2<d)[012120]T(x1<a,x2>d)[012012]T(x1<a,x2<d)

- 이러한 설계에서 개별적인 feature selection은 hyperplane(초평면)형태의 decision boubdary(결정 경계)를 얻는 데 핵심이며, 이는 각 feature의 비율을 결정하는 계수가 있는 특징의 선형 결합으로 일반화할 수 있으며, TabNet은 이러한 기능에 기반하여 신중한 설계를 통해 결정 트리(DTs)의 이점을 누리면서 이를 능가함.
- 데이터로 부터 학습된 sprase한 instance별 feature selection이 진행됨.
- 순차적인 다단계 구조를 구축하여, 각 단계는 선택된 feature에 기반한 결정의 일부가 기여함.
- 선택된 feature에 대해 비선형적인 처리를 통해 학습 능력 향상.
- 앙상블을 모방함.
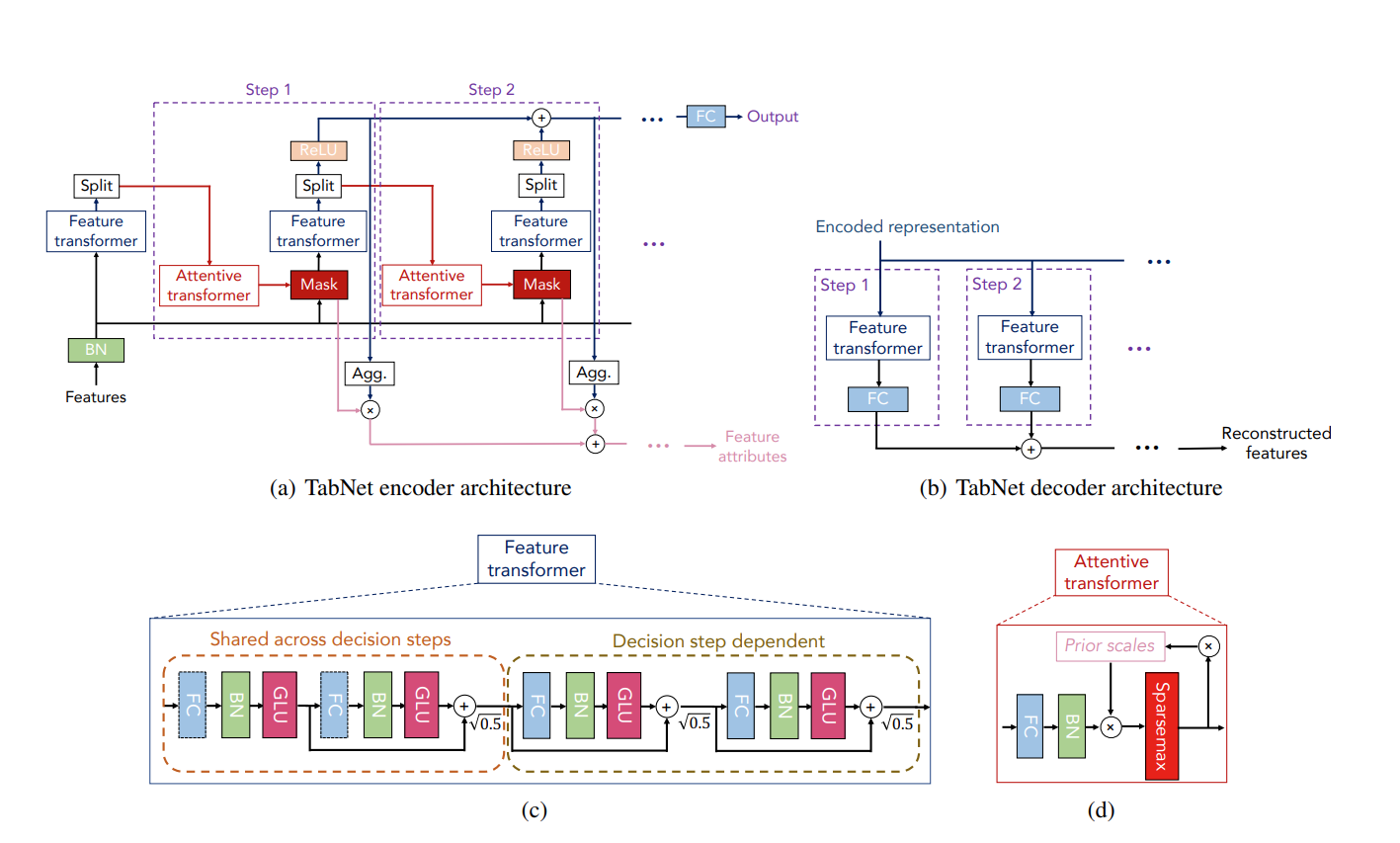
(a) TabNet의 인코더는 feature transformer, attentive transformer, feature masking으로 이루어짐.
split block에서 processed representation(처리된 표현?)은 후속 단계의 Attentive transformer와 전체 출력에 사용됨.
(b) TabNet의 디코더는 feature transformer로 구성됨
(c) feature tramsfpormer 예시 : 4층짜리의 layer이며 fully-connected layer, Batch Normalization, GLU(Gated Linear Unit**)**로 이루어져있음.
GLU(a,b)=a⊗σ(b)
import numpy as np
import torch
x = torch.tensor([[ 0.3548, 2.0516],
[-0.7124, -0.5951],
[-0.0868, 1.6506],
[-0.0592, -0.8288]])
#torch 라이브러리를 이용한 GLU 계산
m = nn.GLU()
output = m(x)
print(output)
#x2는 시그모이드 함수를 통과
x1, x2 = x.chunk(2, dim=1)
x2 = torch.sigmoid(x2)
#요소별로 곱함
glu_output = x1 * x2
print(glu_output)
#tensor([[ 0.3144],
# [-0.2532],
# [-0.0728],
# [-0.0180]])
#tensor([[ 0.3144],
# [-0.2532],
# [-0.0728],
# [-0.0180]])(d) attentive transformer 예 : Prior scale은 이전 decision step들에게 각 feature가 얼마나 사용되었는지를 집계하며, Sparsemax를 사용함.
- https://arxiv.org/abs/1602.02068 [3]
Tensorflow 라이브러리 사용
import tensorflow as tf
import tensorflow_addons as tfa
x = tf.constant([[1.0, 2.0, 3.0], [2.0, 0.5, 0.1]])
# Apply sparsemax activation
sparsemax_output = tfa.activations.sparsemax(x)
print(sparsemax_output)
#tf.Tensor(
#[[0. 0. 1.]
# [1. 0. 0.]], shape=(2, 3), dtype=float32)
#https://www.tensorflow.org/addons/api_docs/python/tfa/activations/sparsemax
직접 구현한 코드
import numpy as np
z = np.array([[1.0, 2.0, 3.0], [2.0, 0.5, 0.1]])
#Sort z
def sprasemax(z):
z_sorted = np.sort(z, axis=1)[:,::-1]
#find K(z)
col_range = np.arange(1, z.shape[1] + 1)
ks = (1 + col_range * z_sorted) > np.cumsum(z_sorted, axis=1)
k_z = np.count_nonzero(ks, axis=1)
#Define t(z)
t_z = (np.sum(z_sorted * ks, axis=1) - 1) / k_z
output = np.maximum(z - t_z.reshape((-1, 1)), 0)
return output
print(sprasemax(z))
#[[0. 0. 1.]
#[1. 0. 0.]]그림 4 : Tabular data를 인코딩 하기 위한 TabNet 아키텍쳐
- Numerical feature(수치형 데이터)는 raw한 데이터 그대로 넣고 categorical features(범주형 데이터)는 학습이 가능한 Embeddings를 사용함
- 이는 범주형 특징을 실수 벡터로 변환하여 딥러닝 모델이 이해할 수 있는 형태로 만드는 과정, 비슷한 범주는 비슷한 임베딩을 가지게 되어 해당 범주의 특성을 잘 반영하게 됨.
- Global Feature Normalization은 따로 적용 되지 않고, Batch Normalization만 적용됨.
- 각 단계마다, D차원의 feature f∈RB×D가 들어감(B는 배치 사이즈).
- TabNet의 인코딩은 연속적인 다단계 처리를 기반으로 하며, 이는 N단계의 결정 단계로 구성되어 있습니다. i번째 단계는 (i - 1)번째 단계에서 처리된 정보를 입력으로 사용하여 어떤 feature를 사용할지 결정하고, 처리된 feature representation(표현?)을 출력하여 전체 결정에 집계시킴.
- 이러한 순차적인 형태의 top-down attention 시각 및 텍스트 데이터 처리(Hudson and Manning 2018), 그리고 강화 학습(Mott 등 2019)에 적용되는 것에서 착안함.
Feature selection : 가장 두드러진 feature를 sparse하게 선택하여 모델이 불필요한 feature에 대한 학습을 줄여 효율적으로 학습할 수 있게 함.
masking은 기본적으로 아래와 같은 식을 따름.
M[i]⋅f
masking은 Attentive Transformer가 사용 이전 단계에서 처리된 feature를 기반으로 얻음.
M[i]는 아래와 같은 식을 따름.
M[i]=sparsemax(P[i−1]⋅hi(a[i−1]))
여기서 sparsemax normalization은 Euclidean projection(유클리드 투영?)을 probabilistic simplex(단순 확률적)으로 대응 시키며, 이는 feature selection과 explainability를 위한 목표에 있어 우수한 성능을 나타냄.
Euclidean projection
x0=argminx||x−x0||2
→ sparsemax normalization가 probabilistic simplex라는 모든 원소가 0 이상이고 모든합이 1 이상인 벡터 공간을 의미하는데 그 공간에 Euclidean projection 한다는 느낌 인듯?
→ 그렇기 때문에 ∑Dj=1M[i]b,j=1 가 성립함
hi는 학습 가능한 함수로, 완전 연결 계층(Fully Connected layer)을 사용하여 표현되며, 이후 배치 정규화(Batch Normalization)가 이어짐.
P[i]는 이전 스케일 항으로, 특정 feature가 이전에 얼마나 사용되었는지를 나타냄.
→ 위에서 언급한 Prior scale
P[i]=i∏j=1(γ−M[j])
γ는 relaxation parameter(완화 매개변수)라고 부름.
이 매개변수는 특정 알고리즘 혹은 기능이 얼마나 유연하게 동작할지를 결정하는 역할을 함 즉 γ는 기능의 '적용 범위' 또는 '적용 강도'를 조절하는 역할을 함.
→γ 값이 1일 때 해당 기능이 활성화되며, γ 값이 증가하면 해당 기능을 여러 결정 단계에서 사용할 수 있다는 것을 의미함.
즉, γ 값이 클수록 기능의 적용 범위가 넓어지거나, 여러 단계에서 동일한 기능을 반복적으로 사용할 수 있는 유연성이 증가.
선택된 feature의 sparsity(희소성)을 추가로 제어하기 위해 엔트로피 형태의 sparsity regularization을 제안함.
Lsparse=Nsteps∑i=1B∑b=1D∑j=1−Mb,j[i]log(Mb,j[i]+ϵ)Nsteps⋅B
ϵ은 로그의 진수가 0이 되지 않도록 하는 작은 양수.
λsparse라는 계수를 사용하여 sparsity regularization를 전체 손실함수에 추가함.
Feature processing
- TabNet에서는 필터된 feature들을 feature transformer를 이용해 처리후, decision(결정 단계)와 후속 단계를 위해 분할함.
- 이 때, [d[i],a[i]]=fi(M[i]⋅f)라는 식이 사용 되며, 여기서 d[i]∈RB×Nd a[i]∈RB×Na.
- parameter를 좀 더 효율적이고 robust(강건한?) 학습을 위해 파라미터가 모든 결정 단계에서 공유되는 그림 (4)에 Shared across decision steps에 해당하는 layer 이고, 결정 단계에 따라 달라지는 그림 (4)에서 Decision step dependent에 해당하는 layer이다.
- 각 FC(Fully connected)뒤에는 BN(batch normalization), GLU(Gated Linear Unit), 그리고 residual connection(잔차 연결)도 있지만, √0.5가 곱해져서 합쳐짐.
- √0.5를 곱하는 이유? 분산을 줄이기 위함.
- 각 FC(Fully connected)뒤에는 BN(batch normalization), GLU(Gated Linear Unit), 그리고 residual connection(잔차 연결)도 있지만, √0.5가 곱해져서 합쳐짐.
- 여기서 batch normalization은 ghost batch normalization이 사용됨.

- Ghost Batch Normalization는 전체 batch를 여러 ghost batch로 나누고, 각 ghost batch에 대해 별도로 normalization을 수행함.
- 최종적으로 (그림 3)과 같은 decision tree와 같이 표현하기 위해 dout=∑Nstepsi=1ReLU(d[i]) 라는 식이 됨.
Interpretability
- TabNet의 features selection mask에서 어떤 feature가 선택 되었는지 알 수 있음.
- 만약 Mb,j[i]=0이라면, b번째 샘플의 j번째 feature은 결정에 기여하지 않아야 함.
- fi가 선형 함수이면, 계수 Mb,j[i]는 fb,j의 feature importance에 해당함.
- 각 decision step이 비선형 처리지만 나중에 결과는 선형 방식으로 결합됨.
- 전체적인 feature importance를 quantify(정량화?)하기 위해 각 decision step에서 상대적인 중요성을 평가 할 수 있는 coefficient(계수)가 필요.
- ηb[i]=∑Ndc=1ReLU(db,c[i])를 제안하여 b번째 샘플의 i번째 decision step에서의 aggregate decision contribution(의사 결정 기여도)를 나타냄.
- 만약 db,c[i]<0이라면, i번째 decision step의 모든 특성들은 전반적인 결정에 대해 0의 기여를 해야 하며, 그 값이 증가함에 따라, 그것은 전반적인 선형 조합에서 더 높은 역할을 함.
Tabular self-supervised learning
- TabNet 표 형식의 특성을 재구성하기 위한 encoder-decoder 구조를 제안합니다.
- 이 디코더는 각 결정 단계에서 특성 변환기와 이어지는 FC 계층으로 구성되며, 출력 값들은 재구성된 특성을 얻기 위해 합산됨.
- 누락된 feature를 다른 열로부터 예측을 하기 위해 binary mask를 S∈{0,1}B×D로 고려함.
- TabNet 인코더는 (1−S)⋅f를 입력으로 받아 재구성된 feature인 S⋅ˆf를 얻음.
- 여기서 논문에선 인코더의 입력이 (1−S)⋅ˆf인데 ˆf은 예측 값 이므로 인코더의 입력으로 들어 갈 수 없는 것 같음.
- reconstruction loss는 최종적으로 아래와 같은 식이 됨.
|S⋅ˆf−S⋅f|2=B∑b=1D∑j=1|ˆfb,jSb,j−fb,jSb,j|2
- feature의 범위가 다를 수 있으므로 모집단 표준편차를 사용하여 normalization을 진행함.
- Sb,j에 대하여 ps는 베르누이 분포 사용.
- 베르누이 분포 : 두 가지 결과만 있는 실험에서 사용되는 확률 분포
- Sb,j에 대하여 ps는 베르누이 분포 사용.
Conclusions
- TabNet은 a sequential attention 메커니즘을 이용하여 각 decision step에서 의미있는 feature를 선택하게 됨.
- 이로 인해 효율적인 학습이 되고 selection masks를 이용한 해석 가능한 의사결정을 제공.
Example Code
TabNet의 코드는 생각보다 Sklearn 형식으로 fit - predict 형식으로 간단함.
Regressor 또한 가능.
https://github.com/dreamquark-ai/tabnet
GitHub - dreamquark-ai/tabnet: PyTorch implementation of TabNet paper : https://arxiv.org/pdf/1908.07442.pdf
PyTorch implementation of TabNet paper : https://arxiv.org/pdf/1908.07442.pdf - GitHub - dreamquark-ai/tabnet: PyTorch implementation of TabNet paper : https://arxiv.org/pdf/1908.07442.pdf
github.com
import numpy as np
import torch
import torch.nn as nn
from sklearn.model_selection import train_test_split
from pytorch_tabnet.tab_model import TabNetClassifier
from sklearn.datasets import load_iris
# Iris 데이터 불러오기
iris = load_iris()
X = iris.data
y = iris.target
# 데이터 분할 (학습 데이터와 테스트 데이터)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.1,
random_state=42, stratify=y)
# TabNet 모델 초기화 및 학습
clf = TabNetClassifier(
#optimizer
optimizer_fn=torch.optim.Adam)
clf.fit(X_train=X_train, y_train=y_train
#validation data
#eval_set=[(X_test, y_test)]
#배치 사이즈
,batch_size=32,
#ghost batch nomalization에 사용되는 ghost(github에는 미니 라고 되어있음) 배치 크기
#virtual_batch_size=4
#eval_metric(평가 함수)
eval_metric=['accuracy'],
#loss function(손실 함수)
loss_fn=nn.CrossEntropyLoss(),
#5번 이상 개선 없을 시 조기 종료, 0은 조기 종료 미설정
patience=0,
#최대 에포크
max_epochs=50,
#남은 마지막 배치 삭제 여부
drop_last=False)
# 모델 성능 평가
test_preds = clf.predict(X_test)
추가로…
해당 논문에서의 TabNet의 결과가 다른 DTs 계열들의 결과보다 너무 좋기 때문에 의구심이 생김.
실제로 해당 논문과 반대의 내용을 띄는 논문들도 존재.
https://www.sciencedirect.com/science/article/abs/pii/S1566253521002360 [5]
https://ieeexplore.ieee.org/abstract/document/9998482 [6]
해당 논문들을 자세히 읽어보진 않았지만 DNN 계열이 아직은 DTs 관련 모델에 비해 성능이 떨어진다는 내용.
논문 내용이 너무 어려워서… 힘들었습니다.
References
[1] Zhang, Mengxiao, et al. "The Local Dimension of Deep Manifold." arXiv preprint arXiv:1711.01573 (2017).
[2] 회사 Notion Research
[3] Martins, Andre, and Ramon Astudillo. "From softmax to sparsemax: A sparse model of attention and multi-label classification." International conference on machine learning. PMLR, 2016.
[4] Hoffer, Elad, Itay Hubara, and Daniel Soudry. "Train longer, generalize better: closing the generalization gap in large batch training of neural networks." Advances in neural information processing systems 30 (2017).
[5] Shwartz-Ziv, Ravid, and Amitai Armon. "Tabular data: Deep learning is not all you need." Information Fusion 81 (2022): 84-90.
[6] Borisov, Vadim, et al. "Deep neural networks and tabular data: A survey." IEEE Transactions on Neural Networks and Learning Systems (2022).




