잡동사니 블로그
K-nearest neighbor(KNN) 본문
지도 학습(Supervised Learning)의 한 종류로서, 데이터 포인트들 간의 거리를 기반으로 패턴을 학습하고 예측하는 알고리즘, 주어진 데이터셋 내에서 가장 가까운 이웃들을 이용하여 새로운 데이터 포인트의 클래스나 값을 예측하는 데 사용.
즉 어떤 데이터가 있으면 그 주변의 이웃 데이터를 살펴본 후 더 많은 데이터가 포함되어 있는 범주로 데이터를 분류.

새로운 데이터 근처에 가장 가까운 k개의 데이터의 레이블 가운데 가장 많이 포함되어있는 범주를 선택하는 알고리즘
k값에 따라 알고리즘의 결과가 바뀔 수 있음(k가 너무 작음: overfitting / k가 너무 큼: underfitting). 즉 적절한 k를 선택하는 것이 중요하며 일반적으로 k값은 홀수를 사용함. 이유는 짝수의 경우, 동점 상황이 발생할 수 있음.
장점
KNN은 단순히 저장되어 있는 데이터들 간 거리를 측정하고 가장 가까운 k개의 데이터를 고르는 작업을 수행하기 때문에 사전 모델링 과정이 없음.
간단하고 직관적인 모델
단점
큰 데이터셋에서는 계산 비용이 증가하며, 예측 속도가 느림.
거리 계산
유클리드 거리 (Euclidean distance)
–점과 점 사이의 일반적인 직선 거리

맨해튼 거리 (Manhattan distance)
–X축, Y축을 따라 간 거리

import matplotlib.pyplot as plt
import numpy as np
# 두 점의 좌표
point1 = np.array([1, 2])
point2 = np.array([4, 6])
# 유클리디안 거리 계산
euclidean_distance = np.linalg.norm(point2 - point1)
# 맨하탄 거리 계산
manhattan_distance = np.sum(np.abs(point2 - point1))
# 그래프 그리기
plt.figure(figsize=(8, 6))
# 점과 거리를 그림
plt.plot([point1[0], point2[0]], [point1[1], point2[1]], marker='o', color='b', label='Points')
plt.plot([point1[0], point2[0]], [point1[1], point2[1]], linestyle='--', color='g', label='Euclidean Distance')
plt.plot([point1[0], point1[0]], [point1[1], point2[1]], linestyle='--', color='r', label='Manhattan Distance')
plt.plot([point1[0], point2[0]], [point2[1], point2[1]], linestyle='--', color='r')
plt.legend()
plt.grid()
plt.show()
구현 코드
import cv2
import numpy as np
from matplotlib import pyplot as plt
from collections import Counter
# 각 데이터의 위치: 25 X 2 크기에 각각 0 ~ 100
trainData = np.random.randint(0, 100, (25, 2)).astype(np.float32)
# 각 데이터는 0 or 1
response = np.random.randint(0, 2, (25, 1)).astype(np.float32)
# 값이 0인 데이터를 각각 화면 (x, y) 위치에 빨간색으로 칠합니다.
red = trainData[response.ravel() == 0]
plt.scatter(red[:, 0], red[:, 1], 80, 'r', '^')
# 값이 1인 데이터를 각각 화면 (x, y) 위치에 파란색으로 칠합니다.
blue = trainData[response.ravel() == 1]
plt.scatter(blue[:, 0], blue[:, 1], 80, 'b', 's')
# (0 ~ 100, 0 ~ 100) 위치의 데이터를 하나 생성해 칠합니다.
newcomer = np.random.randint(0, 100, (1, 2)).astype(np.float32)
plt.scatter(newcomer[:, 0], newcomer[:, 1], 80, 'g', 'o')
#유클리디안 거리를 활용하여 구현한 코드
total=[]
for i in blue :
total.append([i[0],i[1],1])
for i in red :
total.append([i[0],i[1],0])
ans=[]
for i in total :
ans.append([np.sqrt((i[0]-newcomer[0][0])**2 + (i[1]-newcomer[0][1])**2),i[2]])
ans.sort()
answer=ans[:3]
neighbours=[]
dist=[]
for i in answer :
neighbours.append(i[1])
dist.append(i[0])
label_cnt=Counter(neighbours)
if label_cnt[0] > label_cnt[1] :
results=0
else :
results=1
# 가까운 3개를 찾고, 거리를 고려하여 자신을 정합니다.
print("result : ", results)
print("neighbours :", neighbours)
print("distance: ", dist)
print('*'*30)
#cv2를 활용한 k-NN 분류기 생성
knn = cv2.ml.KNearest_create()
knn.train(trainData, cv2.ml.ROW_SAMPLE, response)
# 새로운 데이터를 분류
ret, results, neighbors, dist = knn.findNearest(newcomer, 3)
# 결과 출력
# cv2.ml.knn은 유클리디안 거리 계산에서 sqrt가 빠짐
print("result : ", results)
print("neighbours :", neighbours)
print("distance: ", dist)
print('*'*30)
plt.show()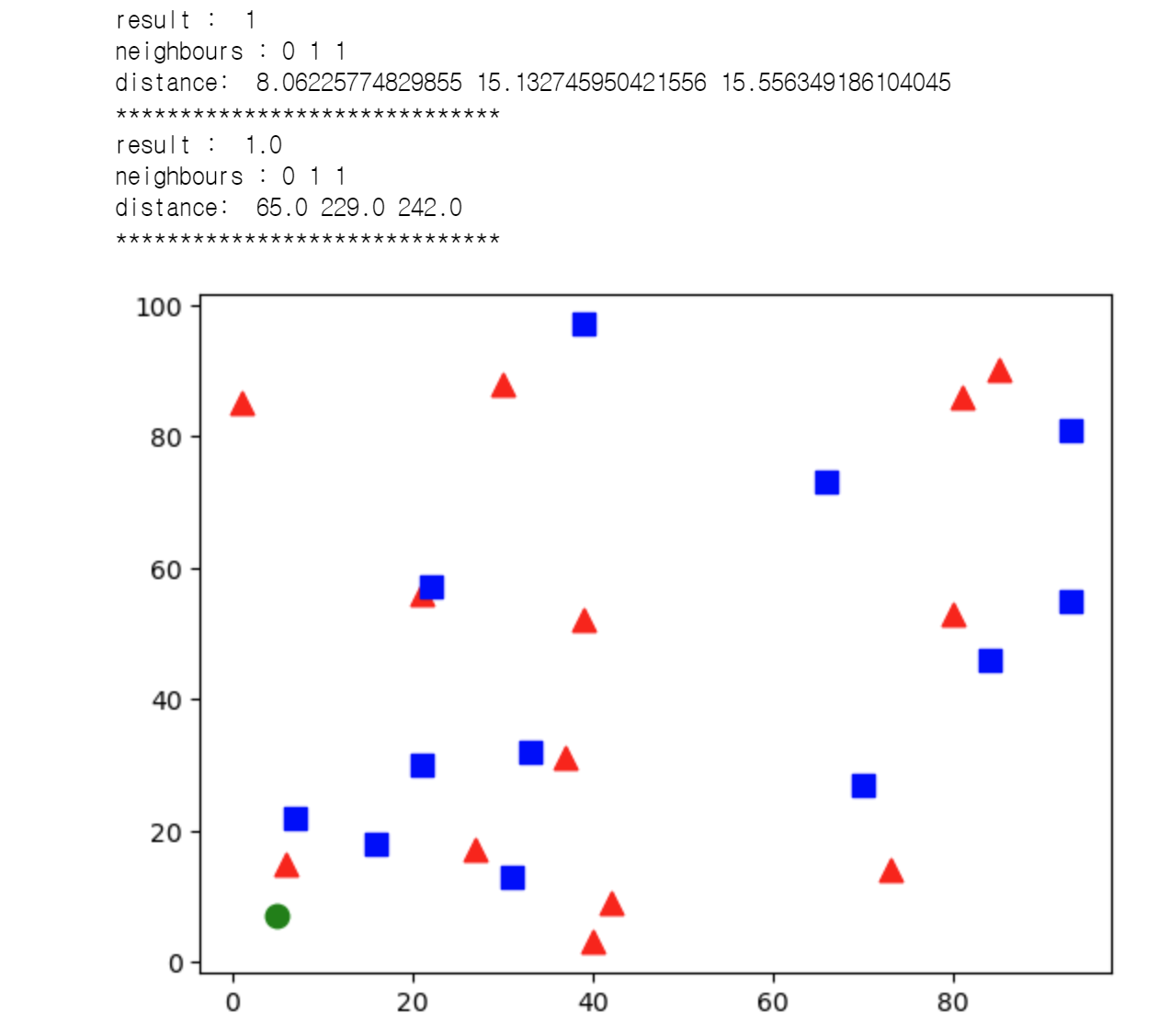
이외에도 sklearn을 사용해서도 구현이 가능함.
from sklearn.neighbors import KNeighborsClassifier
# KNN 모델 생성 및 학습
k = 3
knn = KNeighborsClassifier(n_neighbors=k)
knn.fit(X_train, y_train)
# 예측
y_pred = knn.predict(X_test)'공부용' 카테고리의 다른 글
| [논문 읽기] Effectivs Reinforcement Learning through Evolutionary Surrogate-Assisted Prescription (0) | 2023.09.08 |
|---|---|
| Yolov5 커스텀 데이터 학습 Object detection (0) | 2023.08.20 |
| MediaPipe Pose 사용 (0) | 2023.08.09 |
| [논문 읽기] CutMix(2019) (0) | 2023.07.18 |
| .gitignore 자동생성 (0) | 2023.06.12 |




