잡동사니 블로그
[CS231n] 2장 Image Classification 본문
이미지 분류(Image Classification)란?

이미지를 하나 인식을 하여 시스템상에 있는 미리 결정된 라벨중에 하나를 고름.
사람에게 이것을 구분하기란 쉽지만 컴퓨터에게 이것은 어려운 일.

이유는 컴퓨터에게 이미지는 아주 큰 격자 모양의 숫자집합으로밖에 보이지 않음.

하나의 이미지는 (너비 픽셀 개수, 높이 픽셀 개수, 채널값)으로 구성되며
픽셀(pixel)은 0~255 사이의 밝기를 뜻하며 채널은 색을 표현하기 위한 신호 묶음을 의미하는데 1이면 GrayScale(흑백), 3이면 R(ed),G(reen),B(lue)로 표현한 이미지를 의미함.
import cv2
import matplotlib.pyplot as plt
import itertools
arr = [0,1,2]
nCr = itertools.combinations(arr, 2)
q = sorted(list(nCr),reverse=True)
image_bgr = cv2.imread("/content/drive/MyDrive/25006424_515554352146168_8589974457886441472_n.jpg")
image_rgb = cv2.cvtColor(image_bgr, cv2.COLOR_BGR2RGB)
fig = plt.figure(figsize=(15, 6))
RGB_list = ['Red','Green','Blue']
t=0
for i in RGB_list :
t = t+1
i = image_rgb.copy()
i[:,:,q[t-1][0]] = 0
i[:,:,q[t-1][1]] = 0
if t == 1 :
plt.subplot(1, 4, t)
plt.imshow(image_rgb)
plt.subplot(1, 4, t+1)
plt.imshow(i)

위와 같이 3채널을 가진 하나의 이미지는 빨강 초록 파랑의 이미지가 합쳐 구성된 것.

이미지 분류를 할 때 고민해야 할 점
- Viewpoint Variation (시점 다양성) : 촬영하는 카메라 시점이 변화하면 이미지 픽셀 위치와 값도 모두 변하게 됨.
- Illumination (조명) : 조명, 밝기에 따라 픽셀 값이 달라짐.
- Deformation (변형) : 같은 피사체의 다른 자세에 의한 변형.
- Occlusion (가려짐) : 외부 환경에 의해 물체가 일부분 가려짐.
- Background Clutter (배경 클러터) : Occlusion과 유사하게 외부 환경에 피사체가 섞여 피사체 가려지는 현상.
- Intraclass variation (클래스 내부 클래스의 다양성) : 피사체의 색, 크기, 생김새가 달라도 같은 카테고리 계열은 같은 카테고리로 인식되어야 한다.
- Scale Variation (크기 다양성) : 같은 카테고리라도 사진 혹은 실제로의 크기가 다양한 현상.

사물인식에서의 어떤 한 객체를 인식한다면 직관적이고 명시적인 코드는 존재하지 않음.

가령 하나를 시도해본다면 이미지의 edges(경계선 구분)을 계산하여 고양이의 규칙을 하나하나 명시적인 규칙 집합을 써내려 가보았을 때 두가지의 단점이 존재한다.
1. 이러한 알고리즘은 강인하지 않다. 즉, 예외가 있다면 계속해서 수정해 나가야 할 것이다. 예를 들면 귀가 하나인 고양이와 같은 경우
2. 다른 객체를 인식하는 알고리즘을 짜야 한다면 처음부터 다시 만들어야 한다.
이런 방법은 확장성이 부족하기 때문에 이 세상에 존재하는 다양한 객체들에게 유연하게 적용 가능한 확장성 있느 알고리즘을 만들어야 함.
데이터 기반 (data driven-approach)

앞선 상황을 해결할 방법중 하나인 데이터 중심 접근방법(Data-Driven Approcach)
1. 분류할 데이터 (image)와 정답 데이터 (label) 셋 모으기
2. 분류기(classifier) 훈련(train)시키기
3. 새로운 이미지 (test image)로 분류기 성능 평가하기
최근접이웃 알고리즘(Nearest Neighbor)
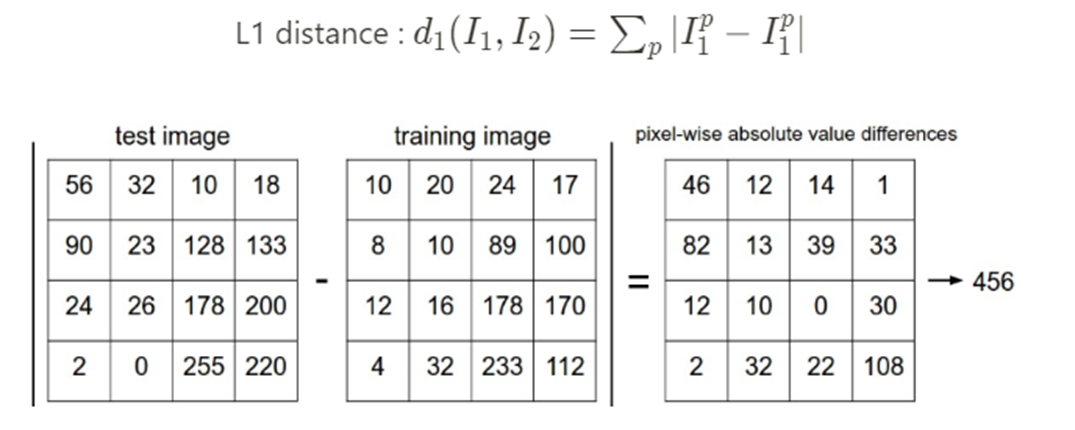
최근접이웃 알고리즘(Nearest Neighbor)은 거리 상 가장 근접한 다른 데이터의 라벨 값을 참조하여 라벨값을 추측한다.
근접한 데이터의 거리를 측정하기 위한 함수는 L1 거리(맨해튼 거리)를 사용하여
두 이미지 벡터 간의 각 픽셀 값의 차이를 비교하고 차이를 모두 합산하는 방식으로 계산함.

그러나 train은 단순히 train set을 저장함으로서 시간복잡도가 O(1)이지만,
predict는 모든 test set에 대해 train set과 길이 비교를 해야함으로 N개의 예제에 대해 O(N)임.
predict(예측)가 오래 걸린다면, 새로운 예제를 예측할 때 마다 그만큼의 시간이 소요됨.
보통 train이 조금 오래 걸리고, predict가 빨리 되는 것을 선호함.
이러한 관점에서 NN 알고리즘은 반대라는 것을 알 수 있음.
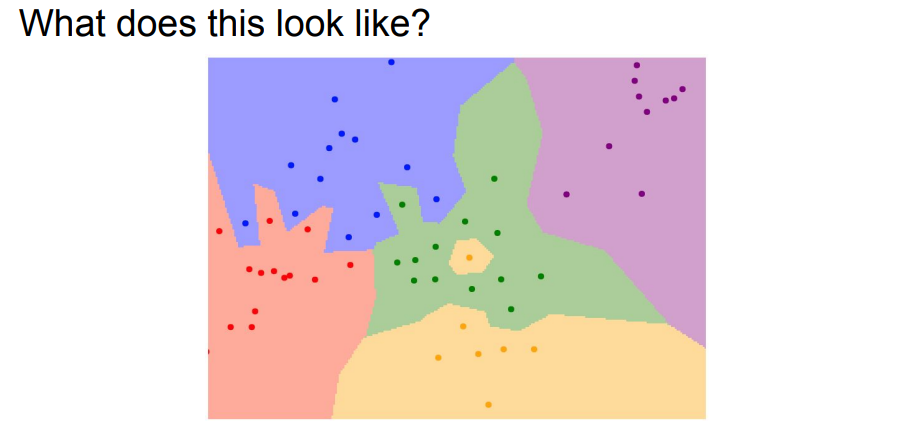
NN알고리즘을 실제로 적용시켰을 때 위와같은 결정경계가 나타난다고 가정했을 때 초록색영역 가운데 있는 노란색점은 가장 가까운 이웃만을 바라보기 때문에 생긴 부분이고, 파란색 영역에 초록색이 있는것은 잡음(noise)이거나 가짜(spurious)일 가능성이 높음.
이러한 문제를 해결하기 위해 조금더 일반화된 버전인 KNN 알고리즘이 나타남.
K-Nearest Neighbors

Distance metric을 이용해서 가까운 이웃을 K개의 만큼찾고, 이웃끼리 투표를 하는 방법이며 가장 많은 득표수를 획득한 레이블로 예측됨. 거리별 가중치를 고려하는 방법도 있으나 득표수로만 예측하는 투표방식이 대게 좋다.
K=1에 비해 K=5인 경우에는 결정경계가 조금 더 부드럽게 된 것을 알 수 있다.
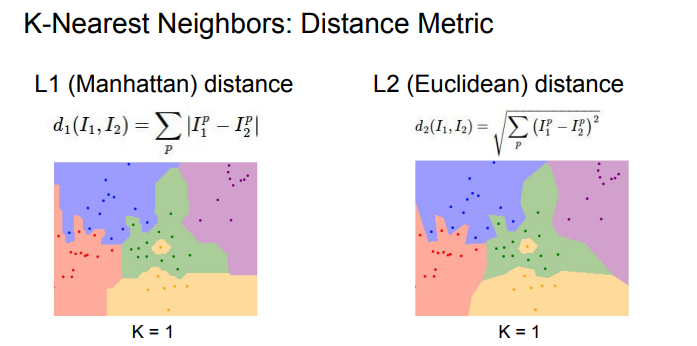
KNN을 사용할 때 결정해야 할 한가지는 Distance Metric인데
L1의 경우 특징 벡터의 각각 요소들이 개별적인 의미를 가지고 있다면 더 잘 어울릴 수 있고,벡터의 요소에 대한 절대값의 합이기 때문에 이상치에 덜 민감함.
L2의 경우 요소들간의 실진적인 의미를 잘 모르는 경우라면 더 잘어울릴 수 있고, 제곱을 더하기 때문에 outlier에 영항을 많이 받음.
하이퍼파라미터 (Hyperparameters)
KNN에서의 하이퍼파라미터는 K와 Distance metric이 될 수 있음.
최적의 하이퍼파라미터를 찾는 가장 간단한 방법은 다양한 하이퍼파라미터 값을 시도해 보고 좋은값을 찾음.
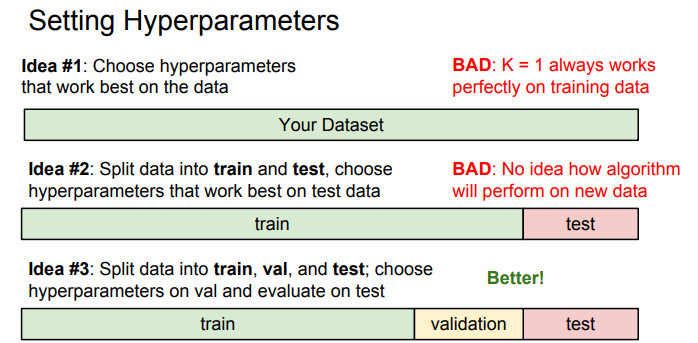
Cross Validation(교차 검증)
idea #1의 경우 Train 데이터만 사용해 하이퍼파리미터를 결정한다면 학습데이터는 가장 잘맞추지만 궁극적으로 기계학습에서는 학습데이터를 얼마나 잘 맞추는지는 중요하지 않으며 우리가 학습시킨 분류기가 한번도 보지 못한 데이터를 얼마나 잘 예측하는지가 중요함.
idea #2의 경우 테스트 셋에서만 잘 동작하는 하이퍼파라미터를 고르게 될 가능성이 있음.
Idea #3의 경우 validation을 이용해 검증을 하여 가장 좋았던 분류기를 테스트 셋에서 단 한번만 수행함.
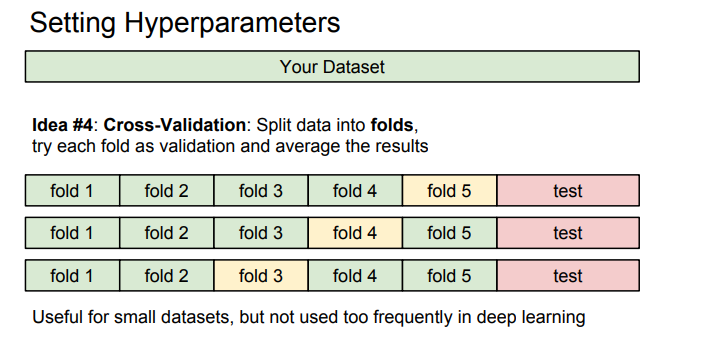
작은 데이터셋에서 많이 사용 되는 방법이며, 테스트 셋을 고정하여 나머지 데이터셋에 대해 train과 validation을 나누어 각 fold마다 train validation을 달리함.
딥러닝의 경우 큰 모델을 학습시킬 때 계산량이 많아 실제로는 잘 쓰지 않는다.
딥러닝 자체가 많은 테스트 데이터셋을 요구하기 때문.
그러나 이미지 분류에서는 KNN을 잘 사용하지 않음.
1) NN 알고리즘과 마찬가지로predict에서의 시간이 느림
2) L1 / L2 distance는 이미지간 유사함을 증명하기 어려움
Linear Classification(선형 분류)
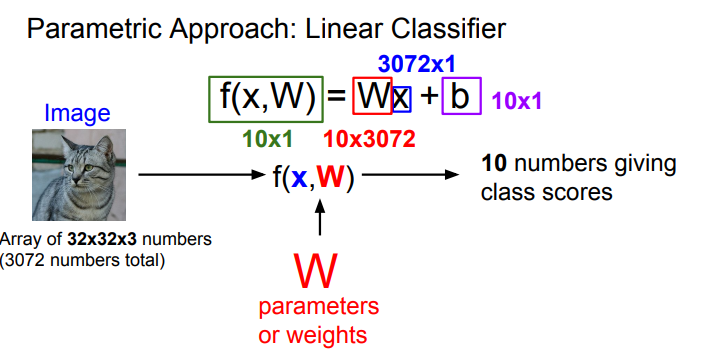
Linear classifier는 "parametric model"의가장 단순한 형태이며 f(x,W) = Wx + b의 식을 가짐.
x: 입력 데이터
w: 가중치
b: bias 입력과 직접 연결되진 않으며 특정 클래스에 우선권을 부여하는 역할
장점은 휴대폰과 같은 기계에서 새로운 데이터의 predict의 속도가 빠름
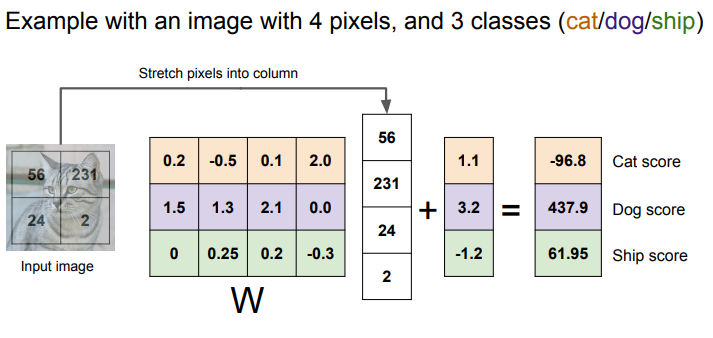
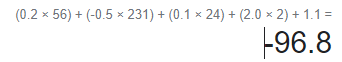
고양이 스코어를 구한다고 할 때 이런식으로 내적을 구하여 마지막에 bias를 더함.

CIFAR-10를 Linear classifier로 학습시킨 가중치 행렬을 시각화 하였을 때, 말의 머리는 두개인 것 처럼 보이는데 이러한 이유는 클래스당 하나의 템플릿 밖에 허용하지 않기 때문.

각 이미지는 고차원 공간의 한 점일 때 Linear classifier는 각 클래스를 구분시켜 주는선형 결정 경계를 그어주는 역할을 함.
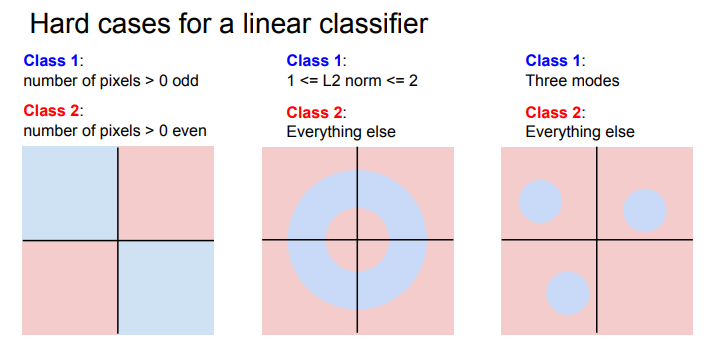
Linear classifier가 풀기 힘든 문제는 parity problem(반전성 문제)거나 Multimodal problem(한 클래스가 다양한 공간에 존재)
이처럼 Linear classifier에는 문제점이 일부 있지만 쉽게 이해하고 해석할 수 있는 알고리즘
'공부용' 카테고리의 다른 글
| Yolov5 커스텀 데이터 학습 Object detection (0) | 2023.08.20 |
|---|---|
| K-nearest neighbor(KNN) (0) | 2023.08.12 |
| MediaPipe Pose 사용 (0) | 2023.08.09 |
| [논문 읽기] CutMix(2019) (0) | 2023.07.18 |
| .gitignore 자동생성 (0) | 2023.06.12 |




